摘要：

Witten方程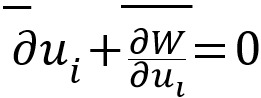，是开始由E.Witten在Landau-Ginzburg A模型中引入的。它的严格数学理论是由范辉军，T.Jarvis和阮勇斌随后创立的，现在称为FJRW理论。FJRW理论在数学和物理上有许多的应用，像Landau-Ginzburg A模型和Landau-Ginzburg B模型的镜像对称，Landau-Ginzburg/Calabi-Yau对应。这个报告将会解释FJRW 理论的基本思想和构造。如同Gromov-Witten理论，FJRW 理论考虑Witten方程在轨形黎曼曲面上的解。FJRW的模空间由Witten方程的解组成，它也有Gromov紧性。一种量子上同调群可以用在这个模空间上计数的方式来定义。为了得到模空间的紧性，我们必须在Witten方程上做大量的分析，这是FJRW理论中最不平凡的一部分。我将介绍获得紧性的关键步骤和一些推广。