(注:部分会议视频已上传,点击下方链接即可查看相关的报告视频)

报告题目及摘要
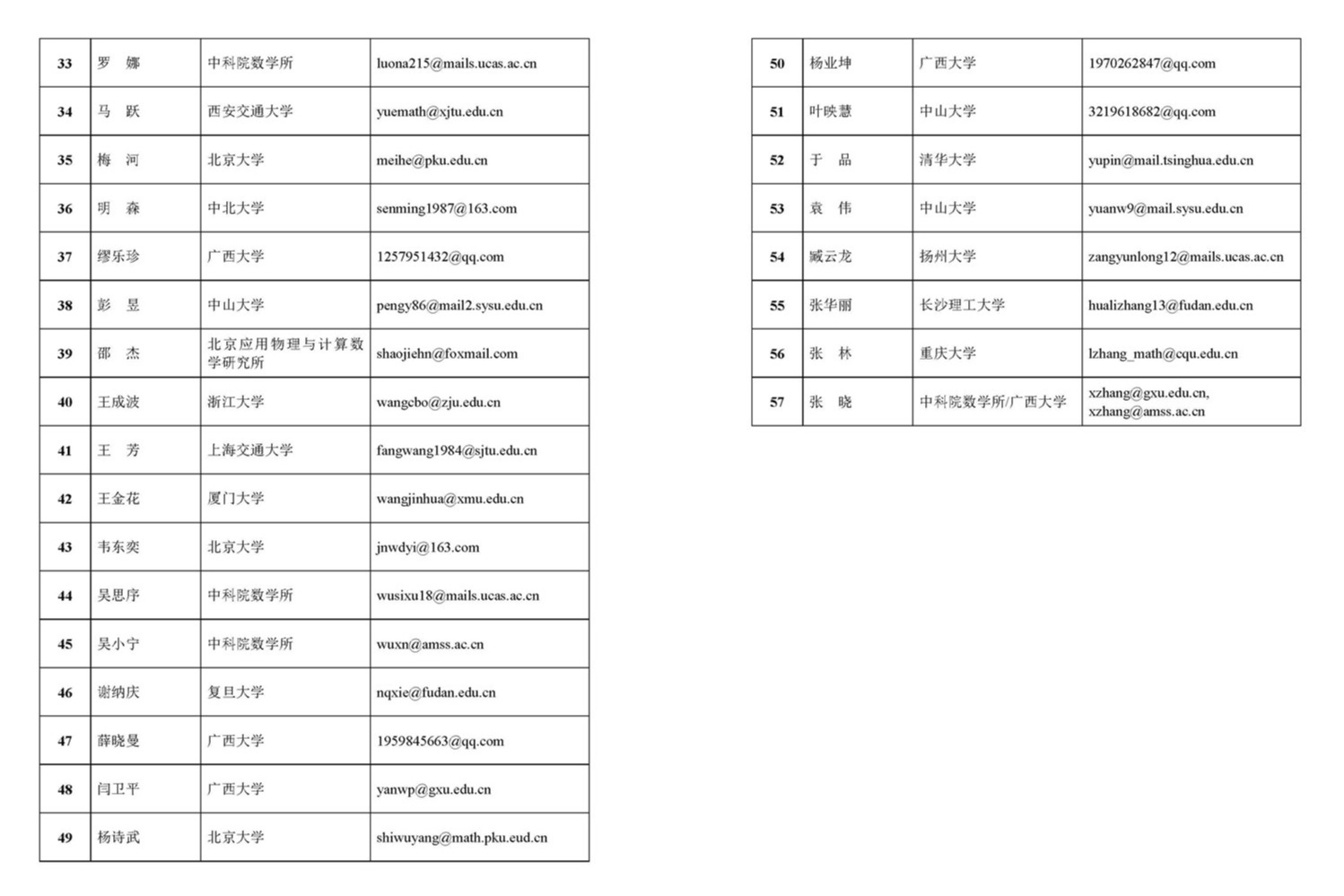
1.袁 伟(中山大学)
Title:Area comparison of hypersurfaces in space forms
Abstract:Mean curvature is one of the most fundamental extrinsic curvature in the theory of submanifold. A natural question is that wether mean curvature can control the area of hypersurfaces. In this talk, we discuss the area comparison with respect to mean curvature for hypersurfaces in space forms. This is a joint work with Professor Sun Jun in Wuhan University.
2.杨诗武(北京大学)点击观看视频
Title:On the global dynamics of Yang-Mills-Higgs equation
Abstract:In this talk, I will talk about the global dynamics of Yang-Mills-Higgs fields in the future of a hyperboloid for data bounded in some weighted energy space larger than the conformal energy space. As application, for the abelian case of Maxwell-Klein-Gordon system, we extend the small data result of Lindblad-Sterbenz to general large data.
3.闫卫平(广西大学)
Title:Global stability dynamics of the timelike extremal hypersurfaces in Minkowski space
Abstract:In this talk, we introduce the relationship between the timelike extremal hypersurfaces and the classical minimal surfaces. This target also gives the long time dynamics of timelike extremal hypersurfaces in Minkowski spacetime with the dimension in [2,7]. In this dimension, the stationary solution of timelike extremal hypersurface equation is the solution of classical minimal surface equation. It only admits the hyperplane solution by Bernstein theorem. We prove that this hyperplane solution as the stationary solution of timelike extremal hypersurface equation is asymptotic stablely by finding the hidden dissipative structure of linearized equation.
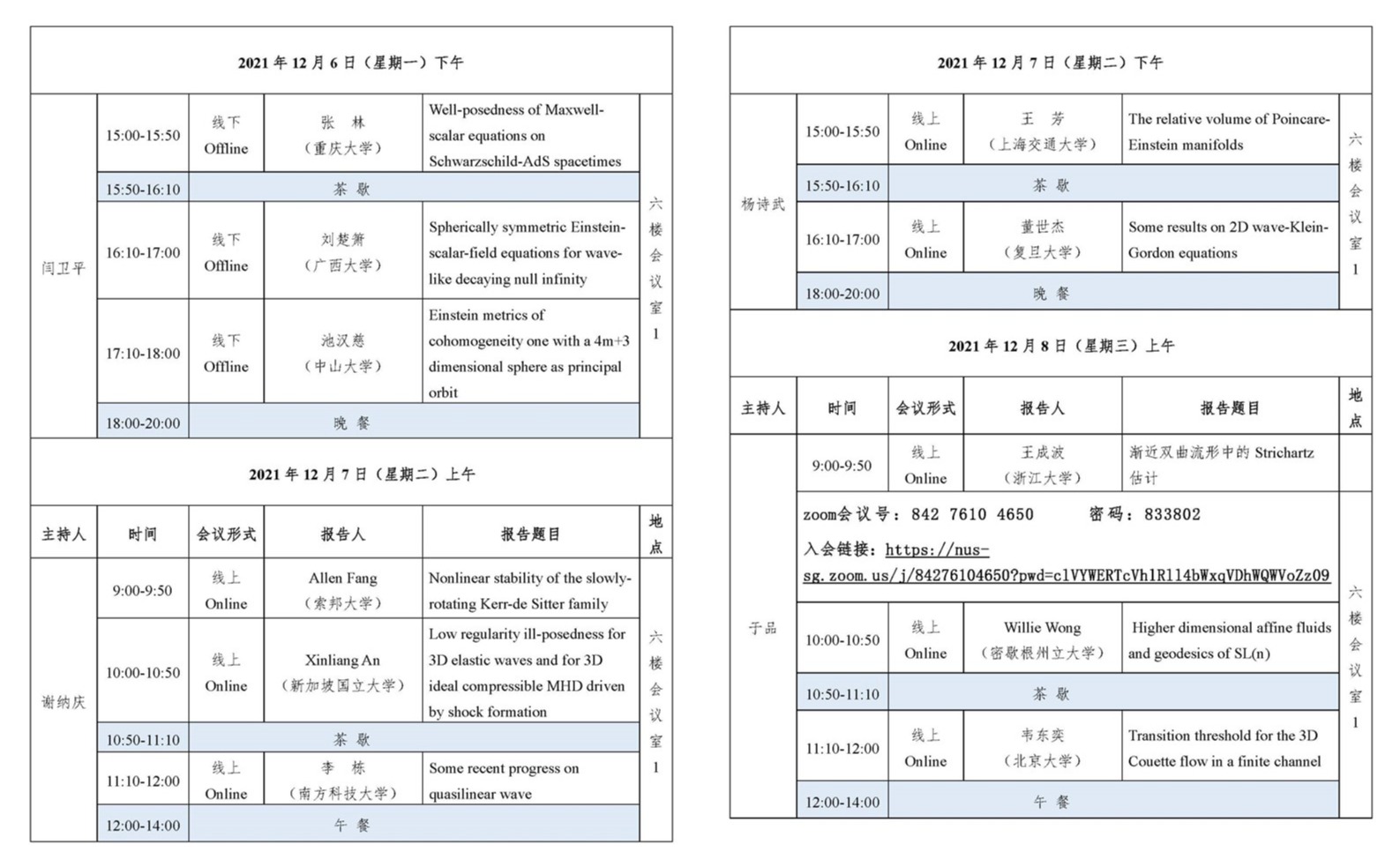
4.张 林(重庆大学)
Title:Well-posedness of Maxwell-scalar equations on Schwarzschild-AdS spacetimes
Abstract:In this talk, I will introduce the local well-posedness for initial-boundary value problems of conformal Maxwell-scalar equations on Schwarzschild-AdS spacetimes. This is a joint work with Prof. Xiaoning Wu.
5.刘楚箫(广西大学)
Title:Spherically symmetric Einstein-scalar-field equations for wave-like decaying null infinity
Abstract:In this talk, we will discuss the spherically symmetric Einstein-scalar field equations for wave-like decaying initial data at null infinity. We show that there exists a unique global solution in (0,∞) and unique generalized solution on [0, ∞)in the sense of Christodoulou. This is a joint work with my supervisor Xiao Zhang.
6.池汉慈(中山大学)点击观看视频
Title:Einstein metrics of cohomogeneity one with a 4m+3 dimensional sphere as principal orbit
Abstract:In this talk, we discuss construction of non-compact complete Einstein metrics with a 4m+3 dimensional sphere as principal orbit. We first discuss the general machinery of using the cohomogeneity one condition to reduce the Einstein equations. Then we present the detail in proving the existence of two continuous 2-parameter families of complete non-positive Einstein metrics with a 4m+3 dimensional sphere as principal orbit. In the end, we will talk about the relation between the new examples to the known ones. This talk is mainly based on the researcher’s work in September 2020.
7.Allen Fang(索邦大学)点击观看视频
Title:Nonlinear stability of the slowly-rotating Kerr-de Sitter family
Abstract:The stability of black hole spacetimes is a critical question in mathematical relativity. The nonlinear stability of the slowly-rotating Kerr-de Sitter family was first proven by Hintz and Vasy in 2016 using microlocal techniques. In my talk, I will present a novel proof of the nonlinear stability of slowly-rotating Kerr-de Sitter that avoids frequency-space techniques outside of a neighborhood of the trapped set. The proof utilizes spectral methods to uncover a spectral gap that yields exponential decay at the linearized level. The exponential decay in the linearized problem is then used in a bootstrap proof to conclude nonlinear stability.
8.Xinliang An(新加坡国立大学)点击观看视频
Title:Low regularity ill-posedness for 3D elastic waves and for 3D ideal compressible MHD driven by shock formation
Abstract:We construct counterexamples to the local existence of low-regularity solutions to elastic wave equations and to the ideal compressible magnetohydrodynamics (MHD) system in three spatial dimensions (3D). Inspired by the recent works of Christodoulou, we generalize Lindblad’s classic results on the scalar wave equation by showing that the Cauchy problems for 3D elastic waves and for 3D MHD system are ill-posed in $H^3(R^3)$ and $H^2(R^3)$, respectively. Both elastic waves and MHD are physical systems with multiple wave-speeds. We further prove that the ill-posedness is caused by instantaneous shock formation, which is characterized by the vanishing of the inverse foliation density. In particular, when the magnetic field is absent in MHD, we also provide a desired low-regularity ill-posedness result for the 3D compressible Euler equations, and it is sharp with respect to the regularity of the fluid velocity. Our proofs for elastic waves and for MHD are based on a coalition of a carefully designed algebraic approach and a geometric approach. To trace the nonlinear interactions of various waves, we algebraically decompose the 3D elastic waves and the 3D ideal MHD equations into $6\times 6$ and $7\times 7$ non-strictly hyperbolic systems. Via detailed calculations, we reveal their hidden subtle structures. With them we give a complete description of solutions’ dynamics up to the earliest singular event, when a shock forms. This talk is based on joint works with Haoyang Chen and Silu Yin.
9.李 栋(南方科技大学)
Title:Some recent progress on quasilinear wave
Abstract:Around 2001 Alinac introduced a new method to settle the global wellposedness of two dimensional quasilinear wave equations with null condtions. The highest norm of the constructed solution admits an upper bound which grows polynomially in time. In this talk I will discuss a group of recent results related to Alinac's blowup at infinity conjecture and several related problems.
10.王 芳(上海交通大学)点击观看视频
Title:The relative volume of Poincare-Einstein manifolds
Abstract:For a Poincare-Einstein manifold, the Bishop-Gromov comparison theorem tells us that the relative volume is a non-increasing function of the geodesic radius. In this talk, I will show that the fractional Yamabe constant at the conformal infinity provides a lower bound for this function. As an application, this implies a gap phenomena and the rigidity theorem.
11.董世杰(复旦大学)点击观看视频
Title:Some results on 2D wave-Klein-Gordon equations
Abstract:I will present some recent results regarding the Dirac-Klein-Gordon equations and the Klein-Gordon-Zakharov equations in two space dimensions, which are or can be transformed into coupled wave-Klein-Gordon equations. These results are joint with Y. Ma (Xi'an) or Z. Wyatt (Cambridge).
12.王成波(浙江大学)点击观看视频
Title:渐近双曲流形中的Strichartz估计
Abstract:本报告中,我们将介绍我们最近与Y. Sire, C. D. Sogge,张军勇一起合作的关于渐近双曲流形中的Strichartz估计及其应用的工作.
13.Willie Wong(密歇根州立大学)点击观看视频
Title: Higher dimensional affine fluids and geodesics of SL(n)
Abstract:One way to understand incompressible fluids is to regard it as constrained free particle transport, a point of view realized in the Euler-Arnol'd formulation of fluid flow as a geodesic motion on the volume-preserving diffeomorphism group. In this talk we will discuss some observations that grew out of the further restriction that the fluid flow be affine. Sideris (2017) observed that such affine fluid flows can be described as geodesics on SL(n) with the Hilbert-Schmidt metric, and studied the properties of several explicit solutions when n = 3. Roberts, Shkoller, and Sideris (2020) then integrated the geodesic equations when n = 2 and obtained a complete classification. In this talk I will present some contrasting results obtained, in collaboration with my students Audrey Rosevear and Samuel Sottile, concerning the geodesic geometry of SL(n) for n > 2, and their applications towards stability and instability of the free boundary incompressible Euler flow.
14.韦东奕(北京大学)点击观看视频
Title:Transition threshold for the 3D Couette flow in a finite channel
Abstract:In this report, I will first state some important progress on linear inviscid damping and enhanced dissipation for shear flows, which play a crucial role in determining the transition threshold. Then I will sketch key ingredients in the proof of transition threshold for 3-D Couette flow in a finite channel. It was proved that if the initial velocity $v_0$ satisfies $\|v_0-(y,0,0)\|_{H^2}\le c_0\text{Re}^{-1}$, then the solution of the 3D Navier-Stokes equations is global in time and does not transition away from the Couette flow, and rapidly converges to a streak solution for $t\gg Re^{\f13}$ due to the mixing-enhanced dissipation effect.
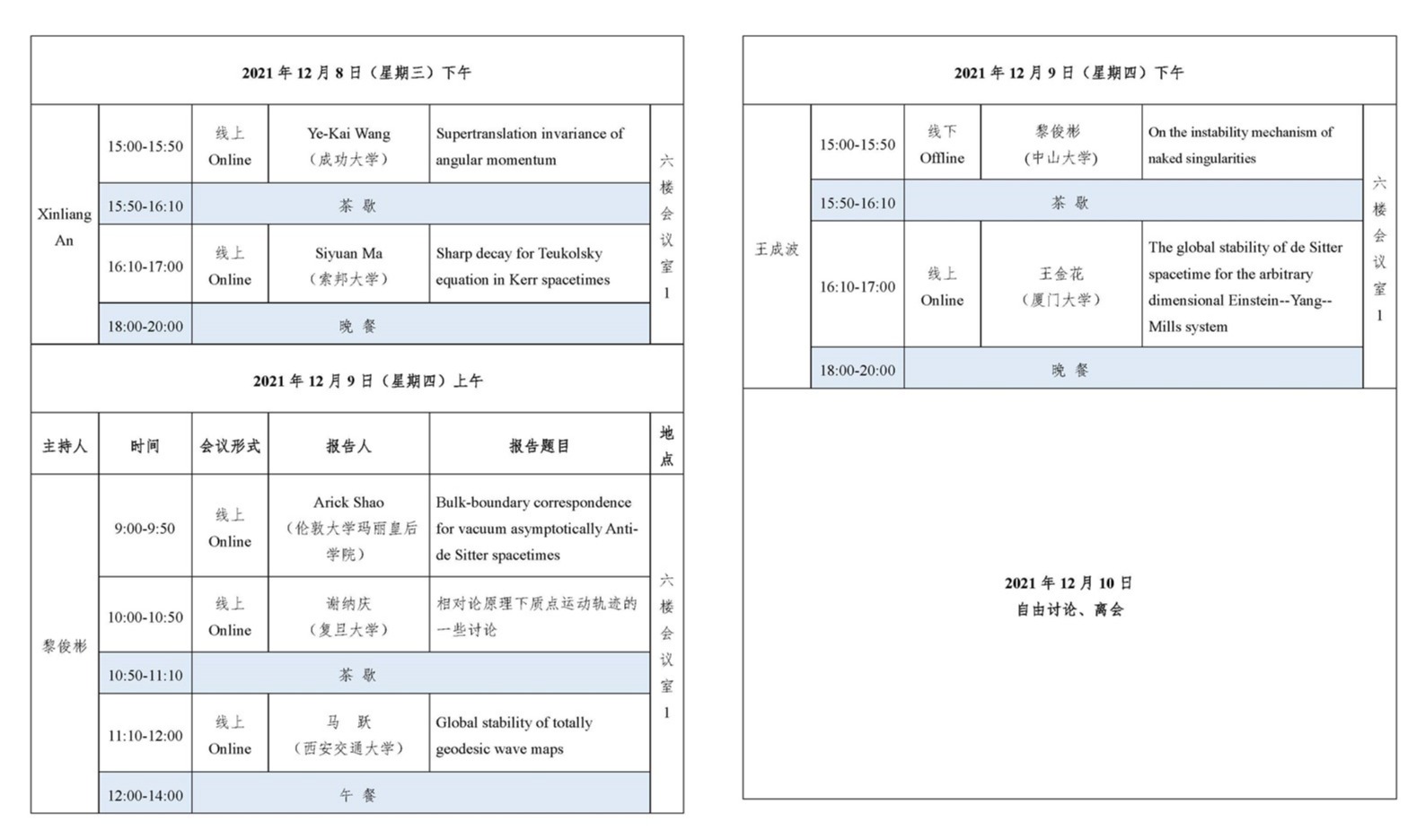
15.Ye-Kai Wang(成功大学)点击观看视频
Title:Supertranslation invariance of angular momentum
Abstract:While there is a well-accepted notion of total energy and linear momentum of gravitational fields, finding a suitable definition of angular momentum is more challenging. The main difficulty is the presence of supertranslations. We discuss how a new definition proposed by Po-Ning Chen, Mu-Tao Wang, and Shing-Tung Yau provides a total flux of angular momentum that is supertranslation invariant. The talk is based on joint work with Po-Ning Chen, Jordan Keller, Mu-Tao Wang, and Shing-Tung Yau.
16.Siyuan Ma(索邦大学)点击观看视频
Title:Sharp decay for Teukolsky equation in Kerr spacetimes
Abstract:Teukolsky equation in Kerr spacetimes governs the dynamics of the spin $s$ components, $s=0,\pm 1, \pm 2$ corresponding to the scalar field, the Maxwell field, and the linearized gravity, respectively. I will discuss recent joint work with L. Zhang on proving the precise asymptotic profiles for these spin $s$ components in Schwarzschild and Kerr spacetimes.
17.Arick Shao(伦敦大学玛丽皇后学院)点击观看视频
Title:Bulk-boundary correspondence for vacuum asymptotically Anti-de Sitter spacetimes
Abstract:"The AdS/CFT conjecture in physics posits the existence of a correspondence between gravitational theories in asymptotically Anti-de Sitter (aAdS) spacetimes and field theories on their conformal boundary. In this presentation, we prove rigorous mathematical statements toward this conjecture. In particular, we show there is a one-to-one correspondence between aAdS solutions of the Einstein-vacuum equations and a suitable space of data on the conformal boundary (consisting of the boundary metric and the boundary stress-energy tensor). We also discuss consequences of this result, as well as the main ingredient behind its proof: a unique continuation property for wave equations on aAdS spacetimes. This is joint work with Gustav Holzegel (and makes use of joint works with Alex McGill and Athanasios Chatzikaleas)."
18.谢纳庆(复旦大学)
Title:相对论原理下质点运动轨迹的一些讨论
Abstract:许多文献都将相对论中所谓的“光速不可超越”表述为“质点的轨迹必须是类时曲线”。这样的表述实际上隐含着一个细微的逻辑问题。描述质点运动的动力系统通常由一个微分方程组表示。根据微分方程解的存在与唯一性定理,给定适当的初始位置与初始速度后,该质点的轨线就完全决定了。我们自然地要问“整条轨线保持类时性”这句话到底是先验假设还是给定初值后的数学结果?在狭义相对论框架下,我们严格证明了,给定质点的初始位置及类时初始4-速度,如果系统的4-外力之Minkowski模长有界,那么质点的运动轨迹是一条容许无穷长固有时的类时曲线。在广义相对论框架下,时空是弯曲的,这个问题将变得异常之复杂。我们也就其中部分困难作非常初步的讨论。本报告的内容基于报告人与吴小宁最近合作的一项工作。
19.马 跃(西安交通大学)
Title:Global stability of totally geodesic wave maps
Abstract:In this presentation I will talk about some recent progress on the global stability problem of totally geodesic wave maps in $\mathbb{R}^{1+2}$. We reformulated the problem when the target space is a general Riemannian manifold (compared with the previous works where the target are supposed to be space forms). With some geometrical observations, we found that the evolution system of the perturbation still enjoys sufficiently nice structure such that the global stability can be established via a global analysis on a type of wave-like systems in $\mathbb{R}^{1+2}$. For this purpose, some techniques originally aimed at wave-Klein-Gordon systems are generalized. Especially, we do not demand the compactness on the support of initial data. This is a joint work with S.-H. Duan.
20.黎俊彬(中山大学)点击观看视频
Title:On the instability mechanism of naked singularities
Abstract:I will give a brief introduction of the weak cosmic censorship, review the proof of the instability of naked singularities in spherical symmetry, and discuss some further related problems.
21.王金花(厦门大学)点击观看视频
Title:The global stability of de Sitter spacetime for the arbitrary dimensional Einstein--Yang--Mills system
Abstract:We establish the non-linear global stability of solutions to the $n$-dimensional ($n\geq 4$) Einstein--Yang--Mills (EYM) system, which continues the local existence of the system in the companion paper (Chao. Liu and Jinhua. Wang, 2021). A new tensorial Fuchsian formulation of the conformal EYM system with temporal gauge is presented and this Fuchsian formulation leads to the global existence. This result generalizes the $4$ dimensional results of Friedrich (J. Differential Geometry, 1991) to the non-conformal invariant (dimension $n>4$) case. This is joint work with Chao. Liu and Todd A. Oliynyk.